.
안녕하세요. 에이치비킴 입니다.
논문명: A Unified Approach to Interpreting Model Predictions (Lundberg, Scott M., and Su-In Lee)
인공지능에서, 제작한 모델이 예측한 결과를 이해하는 것은 굉장히 중요하다 (특정 accuracy가 발생한 이유와 같이).
하지만, 복잡한 모델을 사용하여 (앙상블 및 딥러닝 모델들) large modern dataset에서 높은 정확도를 보이는 경우에는 정확도와 해석가능성 사이에 tension이 발생한다.
이러한 문제를 해결하기 위해, 본 논문에서는 SHAP (SHapley Additive exPlanations)을 제안한다.
SHAP의 특성은 다음과 같다.
1. SHAP은 각각의 특성에 부분적 예측을 통한 중요도를 할당한다.
2. SHAP은 additive feature의 중요도 측정을 통해 새로운 클래스를 정의한다.
3. 클래스별 feature의 특성이 존재한다는 것을 이론적 결과로 (game theory) 입증한다 (Section 3).
본 논문에서는 모델 내부에서 모델의 정확성에 대한 설명을 제안할 수 있는 관점을 연구한다.
본 논문에서는 위 관점을 갖춘 모델을 explanation model, 설명가능한 모델로 정의한다.
본 논문에서는 이를 통해 현존하는 6가지 기법을 통합한 새로운 additive feature attribution methods를 정의한다 (Section 2).
본 논문에서는 SHAP value 기법을 도입하며, SHAP value란 다양한 기법을 통합하여 산출한 feature importance 값을 나타낸다 (Section 4).
본 논문에서는 SHAP value estimation 기법을 제안한다 (Section 5).
f를 original prediction model to be explained, g를 explanation model로 정의한다.
Explanations models는 simplified input인 x^prime을 사용하며, 이는 mapping 함수 [x = h_{x}(x^prime)]를 통해 정의한 값이다.
Local methods는 g(z^prime)~f(h_{x}(z^prime))을 만족시키도록 제작된다.
2개의 변수를 갖는 선형함수 형태의 explanation model이 있다.
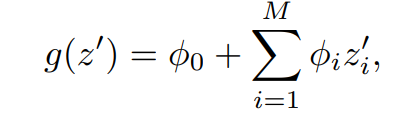
LIME
LIME은 식 1을 사용한 local linear explanation model이자 additive feature attribution method이다.
LIME은 simplified input인 x^prime을 interpretable input, 즉 해석가능한 입력값으로 정의한다.
다른 종류의 mapping 함수를 각기 다른 input spaces에 사용한다.
이미지 분류 작업에서 mapping 함수 h_x는 super pixel을 하나의 이미지로 간주한다.
super pixel의 값을 유지하는 경우에는 1, 주변 픽셀의 평균값으로 전환하는 경우에는 0으로 매핑한다.
식 1의 적절한 phi를 찾기 위해, 다음의 목적함수를 따른다.

식 2에서 omega를 통해 g의 복잡성에 대한 penalty를 부여한다.
LIME에서 g는 식 1을 따르고, L은 squared loss 값이기에, 식 2는 penalized linear regression으로 해결될 수 있다.
DeepLIFT
DeepLIFT는 딥러닝을 위한 재귀 예측 explanation model이다.
각 input x_i에 original value와 반대되는 reference value를 부여한다.
DeepLIFT에서 mapping 함수 [x = h_{x}(x^prime)]를 통해 2개의 변수를 original input으로 변환하며, 1로 매핑되는 경우에는 original value를 부여하고, 0으로 매핑되는 경우에는 reference value를 부여한다.
DeepLIFT에서 reference value는 사용자가 선택한 값으로써, 예측에 도움이 되지 않는 특성을 나타낸다.
Classic Shapley Value Estimation
다음 3개의 기존 기법들은 모델 예측의 설명을 위해 게임이론의 classic equations를 이용하였다.
1. Shapley regression values

2. Shapley sampling values
: 식 3에 sampling approximation을 적용하는 것을 의미한다.
훈련 데이터 셋의 샘플을 통합하여 모델에서 변수를 제거하는 효과를 가진다.
3. Quantitative input influence
고유한 단일 솔루션을 갖도록 하는 3가지 속성이 존재한다.
Properties
Local Accuracy

여기서 x는 h_x(x^prime)를 의미한다.
f(x)는 원 모델의 output을 나타내며, 이것을 설명하기 위한 모델 g가 local accruacy를 만족해야 한다는 속성이다.
Missingness

게임 이론을 활용하기 위해 존재하는 속성이다.
simplified input (x^prime)의 특정 feature가 0이라면, 해당 feature의 영향력 또한 0임을 나타내는 속성이다.
Consistency

서로 다른 모델 f와 f^prime이 존재할 때, f'에서 feature i에 대한 영향력이 f일 때보다 크거나 같다면 f^prime의 explanation model feature i에 대한 계수가 더 큼을 나타내는 속성이다.
위 3가지 속성을 만족할 때, 다음과 같은 정리가 성립한다.
Theorem
Property 1, 2, 3 (Local accuracy, Missingness, Consistency)를 만족할 때, Additive Feature Attribution methods를 통한 explanation model g는 오직 하나 존재한다.

식 7은 cooperative game theory의 결과로 도출되며, 여기서 phi 값은 Shapley values로 알려져있다.
위 3가지 속성을 활용하는 것은 classical Shapley value estimation methods에 적용되었지만, additive feature attribution methods에 적용한 것은 본 논문이 최초로 접근한 방식이다.



