.
안녕하세요 에이치비킴 입니다.
이번 포스팅에서는 채널 부호화(이하 채널 코딩)에 대해서 알아보도록 하겠습니다.
우선 채널 코딩에는 다음과 같은 기법들이 활용되고 있습니다.
1. 선형 블록 부호 (Linear Block code)
1) 순환 부호 (Cyclic code)
2) 순환 덧붙임 검사 (CRC: Cyclic Redundancy Check) - CRC algorithm
2. 길쌈 부호 (Convolutional code)
3. 터보 부호(Turbo code)
4., 5. 는 다음 포스팅에서 다룰 예정입니다.
4. 인터리버 (Interleaver)
5. ARQ 기법 (Automatic Repeat Request)
1) SAW ARQ (Stop-and-Wait ARQ)
2) GBN ARQ (Go-Back-N ARQ)
3) SR ARQ (Selective-Repeat ARQ)
우선 무선통신의 목표는 통신 정확성의 개선입니다. 채널 코딩이란, 송신국 측에서 원 메시지에 미리 정해진 부가 정보를 추가하는 것으로써 이 정보에는 논리적 연관성이 있어야 합니다. 그리고 부가 정보의 도입은, 보다 많은 주파수 대역을 사용하게 되는 것을 의미하죠. 결국, 우리는 채널 코딩을 통해 신호의 대역폭과 전송 전력을 활용하고 최종적으로 비트 오류 발생을 줄이는 것이 목표입니다.
1. 선형 블록 부호
선형 블록 부호는 (n, k) 의 선형 블록 코드를 가집니다. n 과 k 는 각각 전체 비트열과 정보 데이터열의 비트수를 나타냅니다. n - k 은 패리티 비트의 수를 나타내며, 선형 블록 부호에서 전송되는 정보열은 k 의 배수 값을 나타내고, 각각의 k 비트는 n 비트의 부호로 부호화가 이루어집니다. (n, k) 부호에는 2의 n 제곱(2^n) 개의 서로 다른 조합의 부호들이 존재하게 됩니다. 다만, 정보 비트는 k 개를 갖기 때문에 2의 k 제곱(2^k) 개의 조합이 부호로서 허용됩니다.

앞서 n - k 가 패리티 비트의 수를 나타낸다고 했습니다. 여기서, 패리티 비트는 어떻게 구할 수 있을까요?
패리티 비트는 n, k, i (i = 1, 2, 3, ..., k) 그리고 생성함수 g(x) 가 주어졌을 때 정해진 공식을 이용하여 계산할 수 있습니다. 식 1. 에 표현되어 있는 것이 그 식 입니다.


또한 신드롬 벡터 s 라는 것을 구할 수 있는데요. 우리는 신드롬 벡터 값이 0 이라면 오류가 없다고 판단하며, 0 이 아닌 값일 경우 오류가 생긴 것으로 간주합니다. 신드롬 벡터 s 를 구하는 식은 식 2. 에 표현되어 있습니다.

그리고 G 행렬과 H 행렬이 있습니다. 각각 G 행렬은 생성 행렬로, H 행렬은 패리티 확인 행렬로 정의되어있습니다.

식 3. 에서 표현된 것처럼, 정보 비트열과 패리티 비트열의 앞 뒤 순서가 변경되고, 패리티 행렬이 전치 행렬로 바뀌어 활용되는 것을 확인하여야 합니다.
1) 순환 부호 (Cyclic code)
순환 부호는 선형 블록 부호의 종속 부류로서, 부호화가 쉽다는 장점을 가지며 보다 실용적인 구현이 가능한 순환 구조를 갖는다는 특징이 있습니다. 순환 부호에서 n 비트의 부호어는 다음과 같은 다항식으로 표현될 수 있습니다.
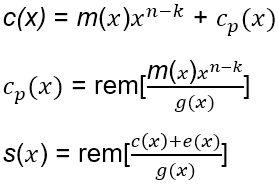
2) 순환 덧붙임 검사 (CRC: Cyclic Redundancy Check)
순환 덧붙임 검사는 데이터 통신 및 기타 직렬 데이터 전송시스템에서 쓰이는 오류 검사 부호입니다. 송신기는 각각의 프레임마다 여분의 n 비트 수열을 추가하며, 추가된 비트 수열을 프레임 검사 수열(FCS) 라고 칭합니다. FCS 내부에는 수신한 프레임에서의 오류를 검출하는 여분의 정보를 담고 있습니다.
CRC 알고리즘이라 불리우는 다음 식에서 Q 는k 비트 길이의 전송 프레임을, F 는 Q 에 추가될 n - k 비트의 FCS 를, J 는 Q 와 F 를 연결하여서 만든 수열을 의미합니다.

Q 는 좌측으로 n - k 비트만큼 이동되며, 그 뒤에 F 가 추가됩니다.
2. 길쌈 부호 (Convolutional code)
길쌈 부호는, 주로 실시간 오류 수정에 사용되며 실제 통신 환경에서 가장 많이 사용되는 채널 부호 중의 하나입니다. 별도의 강력한 수학적 유도를 통하여 개발되었다고 하지만, 본 포스팅에서는 간단한 상태 천이도를 통해 함께 살펴보도록 하겠습니다.

그림 3. 에서 d1, d2, d3 는 각각 입력 데이터와 현재 상태를 나타냅니다. s1 과 s2 는 출력 데이터를 나타내는 것이죠. d1 값은 입력 데이터이기 때문에 매번 바뀌게 되고, d2 와 d3 값은 이전 상태에서 우측으로 한 칸씩 이동하며 변화됩니다. 그림 3. 에서 우측의 표를 보시면 d2, d3 값이 이전 상태에서의 d1, d2, d3 값에서 우측으로 한 칸씩 이동하였다는 것을 알 수 있죠. s1 은 d1, d2, d3 의 모듈로-2 연산, 즉 XOR 연산을 통하여 구해지며 s2 는 d1 과 d3 의 XOR 연산을 통하여 구할 수 있습니다.
3. 터보 부호 (Turbo code)
터보 부호 명칭의 유래는 그 역할이 터보 엔진 구동 원리와 유사하여 이름이 붙어지게 되었다고 합니다. 터보 엔진의 구동 원리에 대하여 간단히 살펴보도록 하죠.
터보 엔진은, 엔진이 뿜어내는 배기가스를 이용해 터빈과 과급기를 동작시킵니다. 즉, 배기가스의 흐름으로 터빈을 돌리고 이 힘으로 과급기를 통해 흡입되는 공기를 추가로 더하는 것이죠.
터보 엔진을 한 문장으로 요약하면, 더 좋은 효율을 내는 모델이라는 것입니다.
우선 터보 부호는 두 개의 동일한 RSC (Recursive Systematic Convolutional) 부호로 구성되어 있습니다. 두 개의 길쌈 부호로 구성되어 있다고 이야기할 수 있습니다. 부호화기와 복호화기는 각 두 개의 부호기 및 복호화기를 갖고 있습니다.

부호화기 측면에서 첫 번째 부호기는 들어온 형태 그대로의 비트열을 사용하고, 두 번째 부호기는 인터리버를 통한 비트열을 사용합니다. 이는 랜덤화를 시키기 위해서 사용되는 것이며, 인터리버에 대해서는 다음포스팅에서 자세히 살펴 볼 예정입니다. 이러한 구성을 거쳐 두 부호기가 만드는 비트들의 상관 관계는 매우 낮습니다.
복호화기 측면에서 두 개의 복호화기 중 하나를 복호화하여 일차적 추정치를 얻습니다. 이에 기반하여 더욱 정교한 추정치를 얻기 위함이며, 두 번째 복호화기의 추정치를 다시 첫째 복호화기의 입력으로 되입력함으로써 전체적인 복호화기의 성능을 높일 수 있게 됩니다.
이번 포스팅에서는 채널 코딩의 기법 세 가지, 선형 블록 부호와 길쌈 부호, 그리고 터보 부호까지 알아보았는데요. 다음 포스팅에서는 인터리버 및 ARQ 기법에 대해서 함께 살펴보도록 하겠습니다.
채널 부호화 (Channel Coding) 및 오류 제어 [2]
. 안녕하세요 에이치비킴 입니다. 이번 포스팅에서는 채널 부호화(이하 채널 코딩)에 대해서 알아보도록 하겠습니다. 우선 채널 코딩에는 다음과 같은 기법들이 활용되고 있습니다. 1. 선형 블록
hyungbinklm.tistory.com
감사합니다.
Reference
[1] https://john.soban.ski/visual-guide-to-forward-error-correction-part-two.html
'무선 & 이동통신 이야기' 카테고리의 다른 글
| 채널 부호화 (Channel Coding) 및 오류 제어 [2] (2) | 2021.07.15 |
|---|---|
| 우분투에 NS-3 (Network Simulator) 설치하기 (2) | 2021.06.24 |

